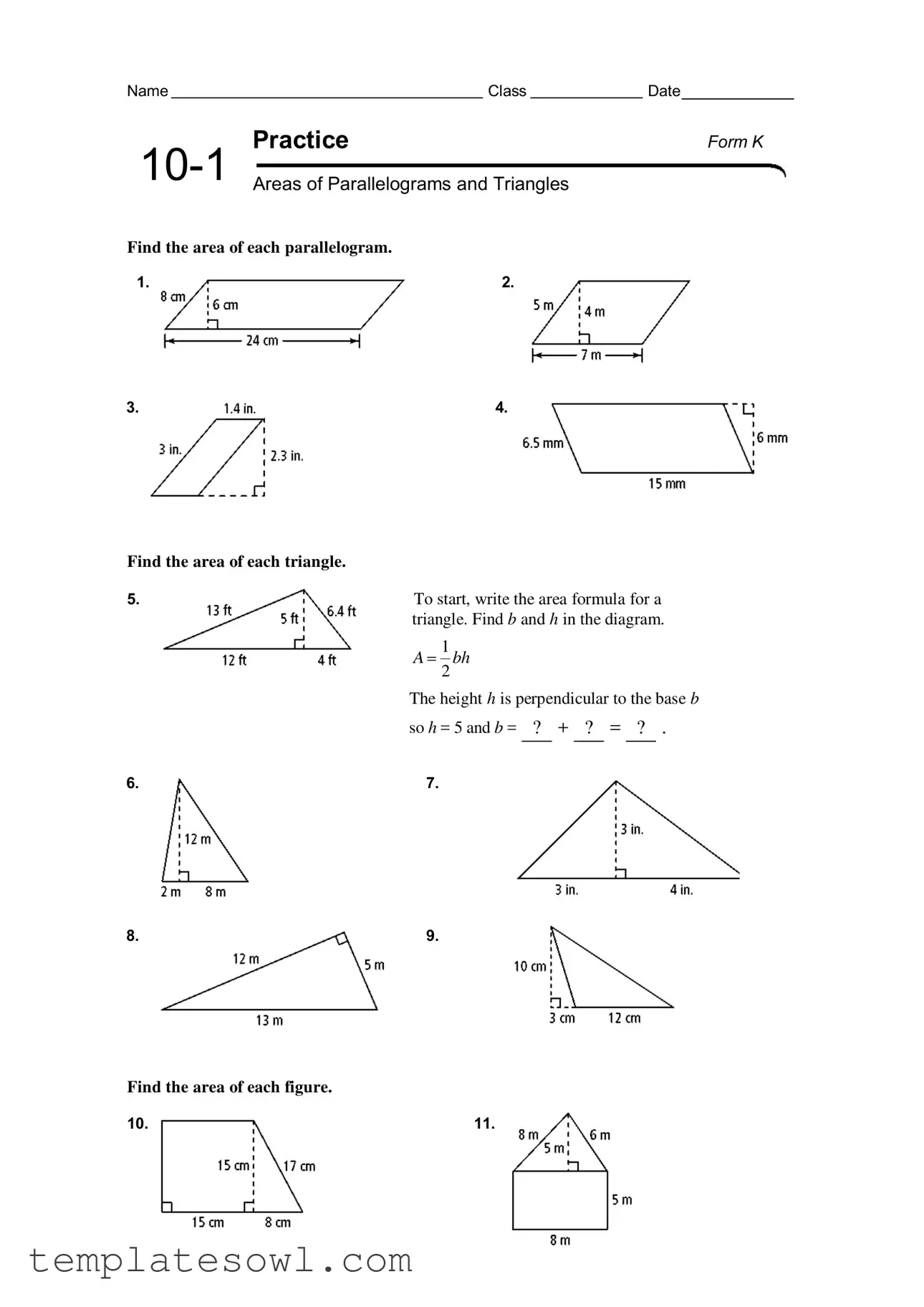
What is the purpose of the Practice 10 1 Areas form?
The Practice 10 1 Areas form is designed to help students practice calculating the area of parallelograms and triangles. It provides various problems where students apply the area formulas specific to these shapes. Completing this form enhances understanding of geometric concepts and improves math skills.
How do I find the area of a parallelogram using this form?
To find the area of a parallelogram, you can use the formula A = B × H, where B is the base and H is the height. The Practice 10 1 Areas form usually provides the necessary dimensions or diagrams to help you identify these values. After finding B and H, simply multiply them to get the area.
What is the area formula for a triangle mentioned in the form?
The area of a triangle is calculated using the formula A = (B × H) / 2. Here, B represents the base of the triangle, and H stands for the height. The Practice form prompts you to first determine these values based on the triangle diagram provided.
Are there specific steps for finding B and H in the triangle diagram?
Yes, finding B and H typically involves identifying the straight edge that serves as the base and measuring the perpendicular distance from this edge to the top vertex of the triangle for the height. The form may give clues or additional information to assist you in this process.
What should I do if I’m unsure about the area calculations?
If you're feeling uncertain, reviewing the area formulas will help. Additionally, there are online resources and videos that can guide you through the steps. Don’t hesitate to ask your teacher or a classmate for clarification. Practice is key, and the more you work through the problems, the more confident you’ll become.
Can I use this form for homework or test preparation?
Absolutely! The Practice 10 1 Areas form is a great tool for homework and test preparation. It provides a solid review of area calculations, reinforcing what you've learned in class. Working through these problems will enhance your skills and ensure you're ready for assessments.