Fill Out Your Statistical Techniques Form

In Chapter 13 we described the relationship between a pair of interval- or ratio-scaled variables. We began the chapter by studying the coefficient of correlation, which measures the strength of the relationship. A coefficient near plus or minus 1.00 (.88 or .78, for example) indicates a very strong linear relationship, whereas a value near 0 (.12 or .18, for example) means that the relationship is weak. Next we developed a procedure to determine a linear equation to express the relationship between the two variables. We referred to this as a regression line. This line describes the rela- tionship between the variables. It also describes the overall pattern of a dependent variable (Y ) to a single independent or explanatory variable (X ).

In multiple linear correlation and regression we use additional independent vari- ables (denoted X1, X2, . . . , and so on) that help us better explain or predict the dependent variable (Y ). Almost all of the ideas we saw in simple linear correlation and regression extend to this more general situation. However, the additional inde- pendent variables do lead to some new considerations. Multiple regression analysis can be used either as a descriptive or as an inferential technique.

Multiple Regression Analysis

The general descriptive form of a multiple linear equation is shown in formula (14–1). We use k to represent the number of independent variables. So k can be any positive integer.

where

a is the intercept, the value of Y when all the X’s are zero.

bj is the amount by which Y changes when that particular Xj increases by one unit, with the values of all other independent variables held constant. The subscript j is simply a label that helps to identify each independent variable; it is not used in any calculations. Usually the subscript is an integer value between 1 and k, which is the number of independent variables. However, the subscript can also be a short or abbreviated label. For example, age could be used as a subscript.

In Chapter 13, the regression analysis described and tested the relationship between

a dependent variable, ˆ and a single independent variable, . The relationship

Y,X

between ˆ and was graphically portrayed by a line. When there are two inde-

Y X

pendent variables, the regression equation is

ˆ

Y a b1X1 b2X2

Because there are two independent variables, this relationship is graphically por- trayed as a plane and is shown in Chart 14–1. The chart shows the residuals as the

difference between the actual and the fitted ˆ on the plane. If a multiple regres-

YY

sion analysis includes more than two independent variables, we cannot use a graph to illustrate the analysis since graphs are limited to three dimensions.

To illustrate the interpretation of the intercept and the two regression coefficients, suppose a vehicle’s mileage per gallon of gasoline is directly related to the octane rat- ing of the gasoline being used (X1) and inversely related to the weight of the automobile (X2). Assume that the regression equation, calculated using statistical software, is:

ˆ 6.3 0.2 0.001

Y X1 X2

X2

the software reports. Note that the software used the variable names or labels associated with each independent variable. The regression equation intercept, a, is labeled as “constant” in the MINITAB output and “intercept” in the Excel output.

In this case the estimated regression equation is:

We can now estimate or predict the January heating cost for a home if we know the mean outside temperature, the inches of insulation, and the age of the furnace. For an example home, the mean outside temperature for the month is 30 degrees

(X1), there are 5 inches of insulation in the attic (X2), and the furnace is 10 years old (X3). By substituting the values for the independent variables:

Y

ˆ 427.194 4.583(30) 14.831(5) 6.101(10) 276.56

The estimated January heating cost is $276.56.

The regression coefficients, and their algebraic signs, also provide information about their individual relationships with the January heating cost. The regression coefficient for mean outside temperature is 4.583. The coefficient is negative and shows an inverse relationship between heating cost and temperature. This is not sur- prising. As the outside temperature increases, the cost to heat the home decreases. The numeric value of the regression coefficient provides more information. If we increase temperature by 1 degree and hold the other two independent variables con- stant, we can estimate a decrease of $4.583 in monthly heating cost. So if the mean temperature in Boston is 25 degrees and it is 35 degrees in Philadelphia, all other things being the same (insulation and age of furnace), we expect the heating cost would be $45.83 less in Philadelphia.

The attic insulation variable also shows an inverse relationship: the more insu- lation in the attic, the less the cost to heat the home. So the negative sign for this coefficient is logical. For each additional inch of insulation, we expect the cost to heat the home to decline $14.83 per month, holding the outside temperature and the age of the furnace constant.

The age of the furnace variable shows a direct relationship. With an older fur- nace, the cost to heat the home increases. Specifically, for each additional year older the furnace is, we expect the cost to increase $6.10 per month.

Self-Review 14–1 There are many restaurants in northeastern South Carolina. They serve beach vacationers in the summer, golfers in the fall and spring, and snowbirds in the winter. Bill and Joyce Tuneall manage several restaurants in the North Jersey area and are considering moving to Myrtle Beach, SC to open a new restaurant. Before making a final decision they wish to investigate existing restaurants and what variables seem to be related to profitability. They gather sample information where profit (reported in $000) is the dependent variable and the independent variables are:

X1 the number of parking spaces near the restaurant.

X2 the number of hours the restaurant is open per week.

X3 the distance from the Pavilion (a landmark in the central area) in Myrtle Beach.

X4 the number of servers employed.

X5 the number of years the current owner has owned the restaurant.

The following is part of the output obtained using statistical software.

(a)What is the amount of profit for a restaurant with 40 parking spaces and that is open 72 hours per week, is 10 miles from the Pavilion, has 20 servers, and has been open 5 years?

(b)Interpret the values of b2 and b3 in the multiple regression equation.

Exercises

1.The director of marketing at Reeves Wholesale Products is studying monthly sales. Three independent variables were selected as estimators of sales: regional population, per

capita income, and regional unemployment rate. The regression equation was computed to be (in dollars):

a.What is the full name of the equation?

b.Interpret the number 64,100.

c.What are the estimated monthly sales for a particular region with a population of 796,000, per capita income of $6,940, and an unemployment rate of 6.0 percent?

2.Thompson Photo Works purchased several new, highly sophisticated processing machines. The production department needed some guidance with respect to qualifica- tions needed by an operator. Is age a factor? Is the length of service as an operator (in years) important? In order to explore further the factors needed to estimate performance on the new processing machines, four variables were listed:

Performance on the new machine is designated Y.

Thirty employees were selected at random. Data were collected for each, and their performances on the new machines were recorded. A few results are:

a.What is this equation called?

b.How many dependent variables are there? Independent variables?

c.What is the number 0.286 called?

d.As age increases by one year, how much does estimated performance on the new machine increase?

e.Carl Knox applied for a job at Photo Works. He has been in the business for six years, and scored 280 on the mechanical aptitude test. Carl’s prior on-the-job per- formance rating is 97, and he is 35 years old. Estimate Carl’s performance on the new machine.

3.A sample of General Mills employees was studied to determine their degree of satis- faction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied, namely, age at the time of first

marriage (X1), annual income (X2), number of children living (X3), value of all assets (X4), status of health in the form of an index (X5), and the average number of social activi- ties per week—such as bowling and dancing (X6). Suppose the multiple regression equation is:

a. What is the estimated index of satisfaction for a person who first married at 18, has an annual income of $26,500, has three children living, has assets of $156,000, has an index of health status of 141, and has 2.5 social activities a week on the average?

b.Which would add more to satisfaction, an additional income of $10,000 a year or two more social activities a week?

4.Cellulon, a manufacturer of home insulation, wants to develop guidelines for builders and consumers on how the thickness of the insulation in the attic of a home and the outdoor

temperature affect natural gas consumption. In the laboratory it varied the insulation thickness and temperature. A few of the findings are:

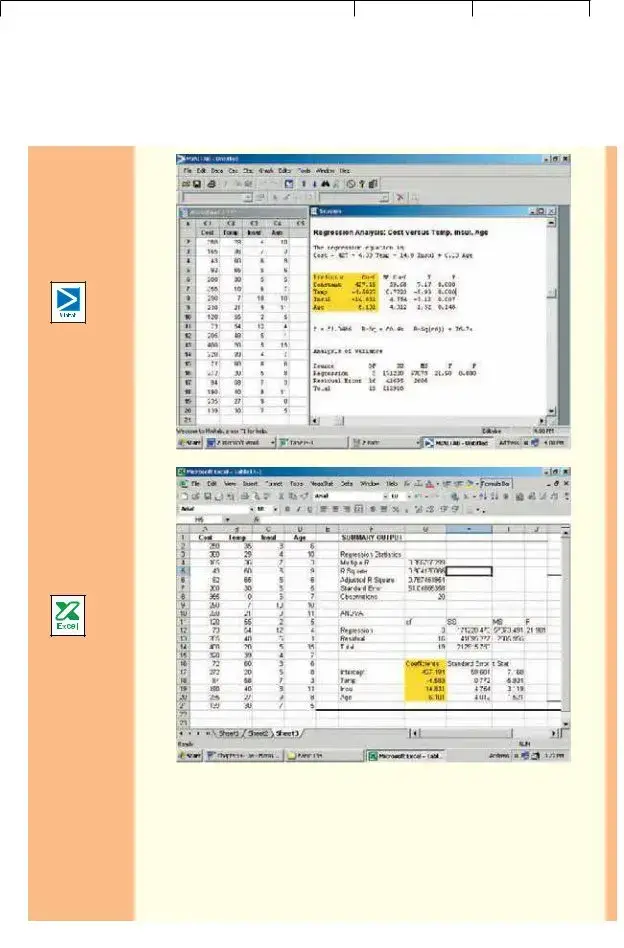
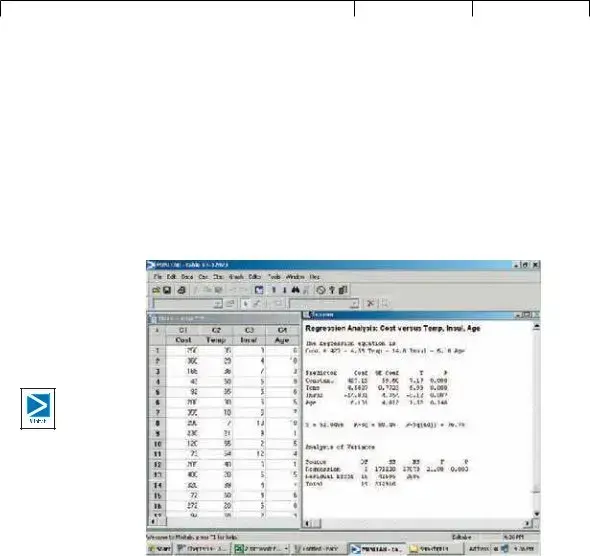
On the basis of the sample results, the regression equation is:

a. How much natural gas can homeowners expect to use per month if they install 6 inches of insulation and the outdoor temperature is 40 degrees F?

b. What effect would installing 7 inches of insulation instead of 6 have on the monthly natural gas consumption (assuming the outdoor temperature remains at 40 degrees F)?

c.Why are the regression coefficients b1 and b2 negative? Is this logical?

How Well Does the Equation Fit the Data?

Once you have the multiple regression equation, it is natural to ask “how well does the equation fit the data?” In linear regression, discussed in the previous chapter, you used summary statistics such as the standard error of estimate and the coef- ficient of determination to describe how effectively a single independent variable explained the variation of the dependent variable. The same procedures, broadened to additional independent variables, are used in multiple regression.

Multiple Standard Error of Estimate

We begin with the multiple standard error of estimate. Recall that the standard error of estimate is comparable to the standard deviation. The standard deviation uses squared deviations from the mean, (Y Y )2, whereas the standard error of

estimate utilizes squared deviations from the regression line, ( ˆ )2. To explain Y Y

the details of the standard error of estimate, refer to the first sampled home in Table 14–1 in the previous example on page 514. The actual heating cost for the first observation, Y, is $250, the outside temperature, X1, is 35 degrees, the depth of insulation, X2, is 3 inches, and the age of the furnace, X3, is 6 years. Using the regression equation developed in the previous section, the estimated heating cost for this home is:

427.194 4.583(35) 14.831(3) 6.101(6)

258.90

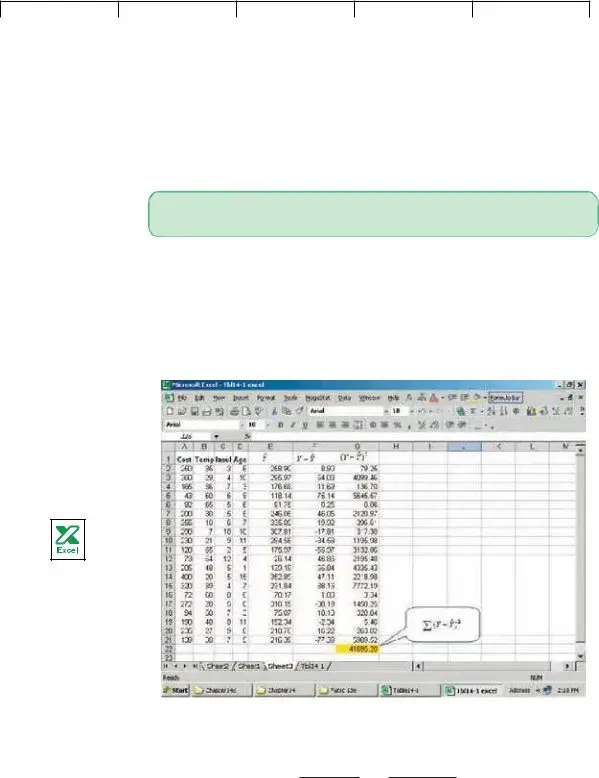
So we would estimate that a home with a mean January outside temperature of 35 degrees, 3 inches of insulation, and a 6-year-old furnace would cost $258.90 to heat. The actual heating cost was $250, so the residual—which is the

250 258.90 8.90. This difference of $8.90 is the random or unexplained error for the first item sampled. Our next step is to square this difference, that is find

other 19 observations and total these squared values. This value is the numerator

of the multiple standard error of estimate. The denominator is the degrees of free- dom, that is n (k 1). The formula for the standard error is:

where

Y is the actual observation.

ˆis the estimated value computed from the regression equation.

Y

n is the number of observations in the sample. k is the number of independent variables.

In this example n 20 and k 3 (three independent variables) and we use the Excel

to rounding.

Since we have 3 independent variables, we identify the multiple standard error as sY.123. The subscripts indicate that three independent variables are being used to estimate Y.

sY.123 Bn (k 1) B20 (3 1) 51.05

How do we interpret the standard error of estimate of 51.05? It is the typical “error” when we use this equation to predict the cost. First, the units are the same as the dependent variable, so the standard error is in dollars, $51.05. Second, we expect the residuals to be approximately normally distributed, so about 68 per- cent of the residuals will be within $51.05 and about 95 percent within

2(51.05) $102.10. Refer to column F of the Excel output, headed ˆ . Of

Y Y the 20 values in this column, 14 (or 70 percent) are less than $51.05 and all are within $102.10, which is very close to the guidelines of 68 percent and 95 percent.

As we said before, the multiple regression computations are long. Luckily, many sta- tistical software systems do the calculations. Most of them report the results in a standard format. The outputs from Excel and MINITAB on page 515 are typical. In particular, they include an analysis of variance (ANOVA) table. The output from MINITAB is repeated here.

Focus on the analysis of variance table. It is similar to the ANOVA table used in Chapter 12. In that chapter the variation was divided into two components: varia- tion due to the treatments and variation due to random error. Here total variation is also separated into two components:

•Variation in the dependent variable explained by the regression model (the inde- pendent variables).

•The residual or error variation. This is the random error due to sampling.

Incidentally, the term residual error will sometimes be called random error or just error. There are three categories identified in the first or Source column in the ANOVA table; namely, the regression or explained variation, the residual or unexplained

variation, and the total variation.

The second column is labeled df in the ANOVA table. It is the degrees of free- dom. The degrees of freedom in the “Regression” row is the number of indepen- dent variables. We let k represent the number of independent variables, so k 3. The degrees of freedom in the “Error” is n (k 1) 20 (3 1) 16. In this example, there are 20 observations so n 20. The total degrees of freedom is n 1 20 1 19.

The heading SS in the third column of the ANOVA table is the sum of squares or the variation.

212,916 41,695 171,220